|

|
Magic, Complexité et Machine de Turing
écrit par zombie33 Le 23 Avril dernier est sortie une publication mathématique traitant de Magic avec en bonus un petit peu d'algorithmique théorique. Pour faire court, c'était Noël avant l'heure. Ce résultat et surtout sa démonstration géniale m'ont très vite poussés à entamer la rédaction d'un article pour Magic-ville sur le sujet. Mon enthousiaste fut de courte durée lorsque j'ai vu le contenu de cet article déformé par la plupart des journaux en ligne manifestement pas assez spécialisé dans le domaine. Ces articles aux titres aussi aguicheurs qu'approximatifs n'ont pu susciter que de la confusion auprès des lecteurs. Au final, en plus de clarifier certaines notions et de présenter la preuve de ce résultat d'une manière qui je l'espère sera accessible à tous, je m'autoriserais quelques digressions plus ou moins grande autour des notions de complexité, d'intelligences artificielles et de résolution de jeu. Bonne lecture à tous. Partie I - Jeux, Complexité et Résolution Peut-être en aviez vous entendu parlé, mais en mars 2016 une intelligence artificielle créée pour jouer au jeu de Go vit le jour. Il s'agit de AlphaGo. Un match en 5 parties fut organisé par Google entre AlphaGo et un grand maitre du Go : Lee Sedol, et bien sur l’événement fut abondamment relayé par les médias. Score finale 4-1 pour Alpha Go. Cet événement eut l'impact d'une petite bombe. Mais Pourquoi donc ? Alors rassurez vous si vous ne savez pas jouer au jeu de Go, il n'y a nul besoin de ça pour comprend la portée de ce qui a été accompli. Pour cela nous devons nous pencher sur la notion de complexité d'un jeu. Le jeu de Go fait partie d'une vaste famille de jeu de stratégie que l'on appelle les jeux finis à informations complètes. Il s'agit de jeux où chaque joueur connaît lors de la prise de décision : - ses possibilités d'action - les possibilités d'action des autres joueurs - les gains résultants de ces actions - les motivations des autres joueurs Enfin dire que le jeu est fini revient à dire qu'à chaque étape les joueurs n'ont qu'un nombre fini d'actions possibles et que nécessairement le jeu s'arrêtera après un certain nombre de coup (en l'occurrence le jeu de go s'arrête lorsque le goban est remplie soit après 361 coups). Depuis l'avènement de l'informatique, on a commencé à concevoir des machines capables de jouer à ces jeux et d'élaborer des stratégies en essayant de prévoir un maximum de coups à l'avance. Ces ordinateurs construisent en réalité un arbre des possibilités où chaque choix fait par tel ou tel joueur crée une nouvelle branche. Grâce à l'informatique, il a été possible de construire l'arbre de certains jeux dans leur totalité. On ne parle donc plus de déterminer les possibilités après 4 ou 5 coups mais bien à partir de la position initiale de déterminer toutes les parties possibles. L'intérêt d'une telle construction est de trouver une stratégie gagnante pour un des joueurs (c'est à dire une stratégie qui lui assurera obligatoirement la victoire quelque soit les choix de son adversaire) ou à l'inverse de démontrer qu'il n'existe pas de telle stratégie et dans ce dernier cas on dira que le jeu est équitable. On appelle cela en mathématiques : Résoudre le jeu. On appelle complexité algorithmique, l'estimation des ressources nécessaires à l’exécution d'un algorithme donné. En ce qui concerne notre sujet, on peut s’intéresser à deux grandeurs qui peuvent attester de la complexité d'un jeu : - le nombre d'états ou de positions possibles du jeu c'est à dire le nombre de nœuds de l'arbre. - le nombre de parties possibles, ce qui correspond au nombre de branches de l'arbre. 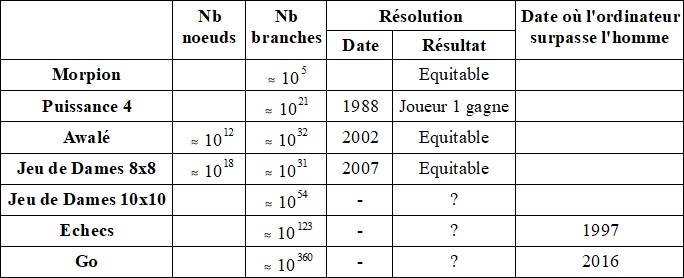 Comme l'atteste le tableau ci-dessus, le jeu de stratégie le plus complexe ayant pu être entièrement résolu à ce jour est le jeu de Dames sur un plateau 8x8. Cette résolution a demandé 18 années de calculs et a permis la modélisation de l'arbre des possibilités dans son ensemble. Avant le jeu de Go, les échecs furent au centre des affrontements entre humain et machine. Et après quelques essais infructueux, la première fois qu'un programme prit l'ascendant sur un grand maître fut en 1997 dans un match opposant Kasparov et Deeper Blue. A l'époque la machine Deeper Blue pesait plus d'une tonne et sa stratégie était entièrement basée sur sa puissance de calcul. Le but étant de prévoir un maximum de coups à l'avance. Il a fallut presque 20 ans pour que l'intelligence artificielle soit capable de franchir le cap immense entre les échecs et le jeu de Go et rivaliser à nouveau avec les experts humains. Cela n'a été possible que grâce à l'avènement d'une révolution informatique récente : Le Machine Learning. C'est un sujet passionnant d'autant qu'après le succès d'Alpha Go en Mars 2016, Google DeepMind lors d'un communiqué a affirmé sa volonté de s'attaquer à de nouveaux jeux dont : Starcraft II (objectif rempli le 29 janvier 2019), Hearstone et Magic the Gathering. Oui Magic a bien été cité, mais hélas je ne vais pas m'aventurer plus loin concernant la notion d'I.A. à Magic car le sujet est vaste et que je ne souhaite pas trop m'éloigné du sujet initial. Quel pourrait bien être la complexité d'un jeu tel que Magic the Gathering ? Pour commencer, il faut bien comprendre que Magic n'est vraiment pas un jeu que l'on peux ranger dans la même catégorie que les précédents. En effet : - Certaines actions à Magic ont des "effets" aléatoires, ne serait-ce que piocher par exemple. - Les joueurs ignorent les possibilités d'action des autres joueurs car leur main est cachée. - Les joueurs ignorent les motivations des autres joueurs car certaines stratégies peuvent pousser un joueur à être bas en point de vie ou à vider sa bibliothèque. - Un joueur peut avoir une infinité d'actions possibles. Cela se produit à chaque fois qu'un joueur doit choisir une valeur pour effectuer une boucle par exemple. - Les parties ne se terminent pas nécessairement. Un miroir de decks composés de terrains et d'Elixir of Immortality ne se termine jamais par exemple alors que ces decks sont pourtant capables de gagner des parties. Le fait que le jeu soit à information incomplète et qu'il y ait une part de hasard dans son déroulement est une grosse différence avec les jeux précédents mais ce n'est pas le plus gros problème car il est toujours possible de raisonner en terme d'espérance. L'introduction de probabilités dans cette affaire semble rendre les rendre les choses encore plus compliquées mais sachez que c'est néanmoins possible d'arriver à des résultats avec des jeux similaires. En 2015 par exemple, des informaticiens de l'université d'Alberta ont réussis à résoudre une variante du Poker à deux joueurs (heads-up en Limit Hold'Em) avec un algorithme nommé Cepheus. Le fait que certaines parties peuvent ne pas se terminer est déjà un peu plus problématique. En effet, cela signifie que notre arbre des possibilités peut être infini et c'est évidemment un problème si on veut en compter les branches ! Ainsi si on souhaite mesurer la complexité de Magic pour la comparer à d'autres jeux, il va falloir trouver un autre moyen de la mesurer. Car ce n'est pas la simple existence de parties infinie qui rend un jeu complexe (la bataille est en effet un exemple de jeu simpliste qui peut ne pas se terminer si les joueurs ne mélangent pas leur défausse quand ils la récupèrent). Précédemment j'ai aussi évoqué le fait qu'un joueur à Magic puisse avoir une infinité de choix d'actions à certains moment. Quand un joueur peut mettre en place une boucle à Magic, il peut choisir de l'effectuer autant de fois qu'il le souhaite. En réalité dans la pratique, créer un million ou un milliard de jetons correspond le plus souvent à un même cas de figure : "créer beaucoup trop de jetons". Il n'empêche que le fait qu'il est possible d'avoir à certains moments de la partie une infinité de choix, peut provoquer des situations très particulières. Prenons l'exemple de deux joueurs possédant tous les deux sur le champ de bataille : Lich, Transcendence et Laboratory Maniac. Un joueur joue Menacing Ogre et la partie se transforme immédiatement en : "Chaque joueur choisit secrètement un nombre et celui qui a choisit le plus grand a gagné". C'est en fait l'exemple classique du jeu qui offre aux joueurs une infinité de choix et pour lequel il n'existe pas de meilleure stratégie. Partie II - Magic est-il vraiment le jeu le plus complexe ? Qu'est-ce qui a été démontré ? Commençons par enfoncer les portes ouvertes : Ce qui a été démontré - n'a pas nécessité l'emploi d'I.A. - n'a rien à voir avec le fait qu'il existe 20 000 cartes à Magic. - n'a rien à voir avec le fait que l'arbre des possibilités à Magic est potentiellement infini. - n'a rien à voir avec le fait que dans certains situations il n'existe pas de stratégie gagnante (voir ci-dessus) Ce qui a été démontré est que que déterminer à l'aide d'un algorithme l'issue d'une partie de Magic dans laquelle toutes les actions sont forcées est impossible. Première conséquence contre-intuitive de ce résultat est qu'il n'existe aucun programme informatique qui, ayant une connaissance complète du jeu, pourrait déterminer l'issue d'une partie Magic. Même en connaissant l'ordre des cartes dans la bibliothèque à chaque instant, en connaissant toutes les décisions successives prises par les joueurs et en supprimant toutes les cartes à effet aléatoire, aucun algorithme ne serait capable de déterminer dans le cas général le gagnant de la partie. Cela signifie que Magic the Gathering échoue à vérifier une des hypothèses couramment formulées par les informaticiens lors de la modélisation de jeux à deux joueurs. Cela suggère que les informaticiens doivent repenser leurs idées sur les jeux, en particulier s’ils espèrent produire une théorie informatique unifiée des jeux. Pour parler de complexité il faut bien comprendre que l'on se place toujours dans le pire des cas et ce que cet article démontre, c'est que pour déterminer le gagnant d'une partie de Magic, le pire des cas de figure n'est pas un cas de figure calculable par ordinateur. Cela signifie que la complexité de Magic est belle est bien au delà de la complexité que l'on retrouve dans la plupart des jeux. Pour être précis, jusqu'à présent Magic est le premier jeu non vidéo-ludique commercialisé à grande échelle pour lequel cette propriété a été démontré et il est fort probable (mais non-démontré) qu'il s'agisse du seul. On remarquera que ce résultat n'a en définitive aucune conséquence particulière pour les joueurs, et qu'il n'en a pas beaucoup plus pour les développeurs d'intelligences artificielles. En effet on se doutait très fortement que créer une I.A. pour jouer à Magic à l'aide d'un arbre des possibilités serait une très mauvaise idée, entre autre parce qu'on sait que c'est une mauvaise idée pour des jeux apparemment plus simple tels que les échecs et le Go. Cet article ne fait que confirmer nos soupçons en affirmant que ce n'est pas juste une mauvaise idée, c'est tout simplement impossible d'y parvenir de cette façon. La preuve de ce résultat à défaut d'être simple est très belle et je ne résiste pas à vous en donner ici les grandes lignes. Toute cette preuve repose sur un résultat d'Alan Turing. Cela peut sembler surprenant mais essayez de suivre aussi, son nom était dans le titre de l'article. Les moins scientifiques d'entre vous auront pu entendre parler d'Alan Turing grâce au film "Imitation Game" où il est interprété par Benedict Cumberbatch, ou encore plus récemment grâce à la pièce de Théâtre aux quatre Molières "La Machine de Turing". Outre avoir déchiffré le code de la machine Enigma lors de la seconde guerre mondiale, Alan Turing est aussi considéré comme le père de l'informatique et des ordinateurs. En effet une machine de Turing n'est ni plus ni moins qu'un ordinateur théorique au fonctionnement basique. C'est grâce à cette notion qu'Alan Turing pu définir formellement la notion d'algorithme et démontra un résultat fascinant connu sous le nom du problème de l'arrêt. Ce résultat stipule qu'il n'existe pas de programme informatique permettant de déterminer si un algorithme va s'arrêter ou non à la simple lecture de ce dernier. On parle de problème indécidable. La démonstration derrière ce résultat n'est pas si complexe mais je laisse aux lecteurs les plus aguerris le loisir de se pencher sur le sujet. Revenons maintenant à notre problème et à son lien avec Magic. L'idée géniale est de montrer que l'on peut créer une partie de Magic dont le déroulé est identique à l’exécution d'un programme sur une machine de Turing. En somme, qu'il est possible de créer une machine de Turing avec des cartes Magic tout en forçant les joueurs à suivre son procédé sans qu'ils puissent à aucun moment interférer avec son fonctionnement ! Et, cerise sur le gâteau, l'issue du match en question ne dépend que d'une chose : savoir si le programme se termine ou non. Etant donné que l'on sait depuis Alan Turing qu'il s'agit d'un problème indécidable, on montre par la même occasion qu'aucun algorithme ne peut déterminer l'issue d'une partie de Magic même lorsque les actions possibles pour les joueurs sont forcées. Partie III - Une machine de Turing en carte Magic Assez tourné autour du pot, il est temps de vous dire ce qu'est exactement une machine de Turing. En théorie une machine de Turing est composée de quatre choses : - d'un ruban comportant une infinité de cases dans lesquelles on pourra inscrire des caractères. - d'une tête de lecture qui peut lire le contenu d'une case mais aussi qui peut y inscrire un nouveau caractère. - d'un registre d'état. Notre machine peut être dans un certain nombre d'états et en fonction de son état fera des actions différentes. - d'une table d'actions qui va décrire quelles actions doit faire la machine à chaque étape. (Ecrire, déplacer la tête de lecture vers la droite ou la gauche du ruban, changer d'état) A première vu cette machine n'a pas l'air de faire grand chose en comparaison de nos ordinateurs. En gros elle écrit des caractères sur un ruban en se déplaçant le long de ce ruban. Au cours de ce programme elle peut potentiellement changer d'état et finalement lorsqu'elle se trouve dans une position pour laquelle elle n'a plus d'instruction elle s'arrête. En réalité, une machine de Turing a une puissance de calcul équivalente à celui de la plupart des langages de programmation tel que le C ou le Java. Oui, rien que ça ! Comment faire pour représenter un ruban avec des cartes Magic ? L'idée sera d'utiliser des créatures sur le champ de bataille à la place des cases. La case sous la tête de lecture sera matérialisés par un jeton 2/2. Les cases situées immédiatement à gauche et à droite seront matérialisées par des jetons 3/3, puis les cases suivantes par des jetons 4/4 et ainsi de suites. Pour bien différencier les cases situées à gauche de la tête de lecture des cases situées à droite de la tête de lecture on considérera que les cases à droite correspondront à des jetons de couleur verte et que les cases à gauche correspondront à des jetons de couleur blanche. Quant à la 2/2 correspondant à la case sous la tête de lecture on a à priori pas de contrainte pour sa couleur. Comment faire pour avoir des caractères dans les cases du ruban ? Pour cela il faudrait pouvoir donner à chaque jeton une caractéristique que l'on associerait à un caractère. L'idée va être de se servir des types de créatures. Il en existe à Magic largement assez pour pouvoir associer à chaque caractère un type de créature. J'en profite pour faire remarquer que la tête de lecture peut changer le caractère de la case qu'elle lit, cela signifie qu'il va falloir trouver un effet qui va affecter uniquement le jeton 2/2 et pas les autres jetons. Lancer un sort tel que Infest semble le moyen idéal. La mort du jeton 2/2 pourrait alors déclencher un trigger créant un nouveau jeton 2/2 d'un autre type ce qui correspondrait exactement au fait de réécrire un caractère sous la tête de lecture. Pour cela pas de soucis il suffit d'utiliser au choix Rotlung Reanimator ou Xathrid Necromancer pour lesquels on aurait modifié les types de créatures et couleurs présents dans leur texte. Comment décaler le ruban vers la droite ou la gauche ? Pour décaler le ruban vers la droite, il suffit d'ajouter un marqueur +1/+1 à toutes les créatures blanches et de mettre un marqueur -1/-1 à toutes les créatures vertes et inversement pour décaler le ruban vers la gauche. On comprend très vite que pour que cette méthode puisse marcher il faut que le jeton 2/2 soit vert lorsque l'on souhaite décaler le ruban vers la droite et qu'il soit blanc lorsqu'on veut décaler le ruban vers la gauche. En réalité le problème doit être pris à l'envers en considérant que la couleur du jeton 2/2 va définir la direction du décalage. Bon tout ce qu'on a fait là n'est que théorique et il faut maintenant arriver à construire cela dans une vraie partie de Magic et mettre les joueurs dans une situation où ils seront forcés d’exécuter le programme de notre choix. En fait toutes toutes les cartes dont on va avoir besoin pour mettre en place cette situation seront dans le deck du premier joueur la bien nommée Alice et celle-ci va créer notre machine de Turing au premier tour à condition qu'elle ait une main de départ parfaite. Et pour arriver à ça on va avoir besoin d'utiliser seulement 42 cartes différentes sur les 20 000 existantes. Voici la decklist d'Alice :
C'est parti ! Alice joue Ancient Tomb et trois Lotus Petals afin de jouer Grim Monolith et Power Artifact afin de générer une quantité arbitrairement grande de mana incolore. Puis Staff of Domination permet de piocher la totalité du deck et Gemstone Array fournit le mana coloré nécessaire pour jouer tous les sorts. A partir de là on a quelques cartes qui vont aider à la mise en place des choses : - Djinn Illuminatus et Reito Lantern nous permettent de jouer tout nos sorts autant de fois qu'on le veut. - Memnarch nous permet de transformer tous nos permanents en artefacts - Stolen Identity nous permet du coup de faire autant de copies qu'on le souhaite de tous nos permanents. - Donate nous permet de donner à notre adversaire tous les permanents que l'on souhaite. - Artificial Evolution et Glamerdye vont permettre de modifier les textes à notre guise des permanents et Prismatic Lace de changer leur couleur. - La bibliothèque de Bob et la main de Bob vont être entièrement exilées avec Fathom Feeder, Karn Liberated et Capsize (ciblant Karn). Grâce à Donate on va donner à Bob un certain nombre de permanents : Tout d'abord 31 Rotlung Reanimator et 7 Xathrid Necromancer dont les textes (types et couleurs) ont tous été soigneusement modifiés pour créer la table d'action de notre machine de Turing. En effet comme dit précédemment, on souhaite que lorsqu'un jeton 2/2 d'un certain type meurt, un jeton d'un autre type particulier soit créé et qu'il ait la couleur de notre choix. Tout ceci peut en effet être soigneusement préparé en amont grâce à Artificial Evolution et Glamerdye. Et qu'en est-il des jetons qui vont former la bande infinie de notre machine ? Et bien ces jetons sont créés à l'aide de Riptide Replicator et Capsize. Ainsi donc la table des actions ainsi que le ruban sont maintenant sous le contrôle de Bob, mais on ne va pas s'arrêter là. A côté de cette partie technique donc, on donne à Bob 5 autres permanents : Wild Evocation, Recycle, Privileged Position, Blazing Archon, Vigor. Bob va ainsi se retrouver dans une situation un peu délicate. Il n'a aucune carte en main ou en bibliothèque mais ne meurt pas à la pioche parce qu'il contrôle Recycle. Il n'a pas non plus de mana ou de capacité à activer. Enfin il ne pourra pas non plus attaquer Alice avec ses créatures car celle-ci possède aussi comme on va le voir un Blazing Archon. En définitive Bob va donc demeurer simple spectateur pour le reste de la partie. Du côté d'Alice il y a aussi une mise en place particulière et complexe comportant : - 36 Cloak of Invisibility enchantant 7 Xathrid Necromancer et 29 Rotlung Reanimator de Bob. On reviendra sur le rôle de ces auras plus tard mais vous vous doutez bien qu'elles vont jouer un rôle important. - 2 Shared Triumph, 2 Rotlung Reanimator, 1 Fungus Sliver, 1 Steely Resolve avec des types modifiés dans le texte. - 2 Dread of Night avec la couleur modifié. A côté de ça, Alice contrôle aussi quelques permanents auxquels on va s'intéresser : Wheel of Sun and Moon l'enchantant, Vigor, Mesmeric Orb, Ancient Tomb, Prismatic Omen, Choke et bien entendu Blazing Archon. En plus de ça Alice aura pris soin de cibler toutes les créatures avec Olivia Voldaren pour leur mettre un marqueur +1/+1 et leur donner un type commun. Enfin pour que la mise en place soit complète il faut que la bibliothèque d'Alice contienne dans cet ordre : Cleansing Beam, Coalition Victory, Soul Snuffers, placés ainsi grâce à Reito Lantern et seul doit rester dans sa main Infest. Tous les autres permanents ayant été exilés à l'aide de Karn Liberated et Capsize (Karn pouvant exiler aussi Capsize et lui même). Bien ! Regardons ce qu'il se passe maintenant du côté d'Alice. - Tout d'abord, Bob contrôle un Blazing Archon donc Alice ne peut pas l'attaquer pour gagner la partie. - Ensuite Alice contrôle un terrain : Ancient Tomb. Ce dernier est même un terrain de tous les types grâce Prismatic Omen mais hélas il ne se dégage pas à cause de Choke. Ainsi Alice tout comme Bob ne peut produire aucun mana. - Alice a une carte en main qu'elle sera obligée de jouer à son upkeep à cause de Wild Evocation contrôlé par Bob. Une fois sa carte jouée, elle ira en dessous de sa bibliothèque puisqu'Alice est enchantée par Wheel of Sun and Moon ce qui l'obligera à jouer inlassablement les même cartes sans avoir non plus le moindre choix à effectuer jusqu'à la fin de la partie. Le programme se lance donc et les joueurs ne peuvent qu'assister impuissants au déroulement de l'algorithme et voir quel destin il leur réserve. Tour 1 : Au début de son entretien, Alice lance Infest. Elle va en réalité tuer ainsi l'unique jeton 2/2 contrôlé par Bob. Ce dernier suivant son type de créature va déclencher la capacité d'un Rotlung Reanimator ou d'un Xathrid Necromancer spécifique qui va créer un nouveau jeton d'une couleur (soit vert soit blanc), d'un type spécifique, soit dégagé, soit engagé. Ce jeton nouvellement créé va alors se retrouver enchanté par Illusory Gains et arriver sous le contrôle d'Alice. Vous l'aurez compris ce jeton donc sous le contrôle d'Alice correspond au jeton sous la tête de lecture. Je rappelle au passage que Infest n'a tué aucun Rotlung Reanimator ou Xathrid Necromancer car ces derniers ont un marqueur +1/+1 sur eux grâce à Olivia Voldaren. Enfin lors de sa phase de pioche Alice va piocher Cleansing Beam. Tour 2 : A la phase de dégagement d'Alice le jeton enchanté par Illusory Gains va se dégager s'il était engagé et se faisant va meuler Alice d'une carte à cause de Mesmeric Orb, et donc Coalition Victory va se retrouver en dessous de la bibliothèque. On reviendra sur les conséquences de ce trigger plus tard lorsqu'il a lieu. Alice doit lancer maintenant Cleansing Beam et doit donc choisir une cible. Seulement grâce à Olivia Voldaren, toutes les créatures du champ de bataille partagent un même type de créature et ce type est justement celui que l'on a donné à Steely Resolve pour que ces créatures aient le linceul. Les créatures de Bob quand à elles ne peuvent pas être ciblées car il contrôle Privileged Position. Cela ne laisse qu'une seule cible valide pour Alice : le jeton enchantée par Illusory Gains qui vient d'arriver sous son contrôle. Comme dit précédemment, ce jeton est soit vert soit blanc. Comme Alice et Bob possèdent tous deux Vigor à la résolution de Cleansing Beam, ils vont placer deux marqueurs +1/+1 sur toutes les créatures qu'ils contrôlent qui sont de la même couleur que ce jeton. Lors de sa phase de pioche, Alice pioche Coalition Victory si la carte n'a pas été mise en dessous de sa bibliothèque, et dans le cas contraire elle pioche Soul Snuffers Tour 3 : - Si Coalition Victory a été meulé au tour précédant, Alice lance Soul Snuffers qui met un marqueur -1/-1 sur toutes les créatures. Finalement, entre ce tour et le tour précédant, toutes les créatures d'une couleur ont gagné -1/-1 et toutes celles de l'autre couleur ont gagné +1/+1. Il s'agit du décalage du ruban vers la droite ou la gauche tel qu'on l'a évoqué précédemment qui a lieu ici. Le hic c'est qu'à force de mettre des marqueurs -1/-1 sur toutes nos créatures, on risque de tuer nos créatures. Pour les sauver rien de plus simple, on leur donne à la fois la couleur verte et la couleur blanche avec Prismatic Lace et donc il recevront toujours deux marqueurs +1/+1 avant de recevoir leur marqueur -1/-1 ce qui les sauvera. Voilà qui marche bien, mais pas pour Vigor car son effet qui ajoute des marqueurs ne fonctionne pas sur lui même... C'est à ce niveau là qu'intervient Fungus Sliver. Il suffit de changer le type de créature dans son texte par Incarnation et là on est enfin bon. - Si Coalition Victory n'a pas été meulé, alors Soul Snuffers est joué lors d'un tour 4. Cela crée donc un cycle de longueur 4 si le jeton est arrivé dégagé ou de longueur 3 si le jeton est arrivé engagé. L'intérêt de ce décalage est de modifier l'état de la machine de Turing. En effet après un cycle de longueur impair les Rotlung Reanimator et Xathrid Necromancer qui seront déphasés par les Cloak of Invisibility ne sont plus les mêmes ! C'est avec cette utilisation astucieuse du déphasage que l'on obtient deux états pour notre machine. Ce changement d'état est donc prévu dans la table des actions par l'utilisation de Xathrid Necromancer plutôt que de Rotlung Reanimator. Et il se trouve que deux états différents étaient justement ce qu'il fallait pour cette preuve. Mais qu'en est-il de la fin de partie ? Et bien parmi tous les caractères encodés par notre machine de Turing il y a un symbole en particulier qui correspond à un symbole d'arrêt. Ce type de créature lorsqu'il est mis dans un cimetière crée un jeton particulier dégagé de couleur bleu chez Alice. Or Alice possède grâce à Prismatic Lace déjà des permanents rouges, verts, noirs et blancs mais aucun bleu ! Aussi grâce à Prismatic Omen Alice possède aussi un terrain de chaque type. Ainsi lorsqu'elle lancera Victory Coalition elle gagnera la partie. Si en revanche ce programme ne s'arrête pas alors selon les règles de Magic la partie se termine par un Match nul. Ainsi l'issu de la partie dépend uniquement de la faculté qu'à un certain programme à s'arrêter. J'ai en définitive volontairement passé sous silence certaines parties techniques (oui, oui...) de cette démonstration mathématique pas comme les autres et pour tout ceux qui souhaiteraient lire la publication originale, je vous renvoie vers les liens externes situés à la fin de cet article. J'espère néanmoins vous avoir donné une bonne idée de ce qui a été démontré et comment cela a été démontré. Appendice - Un jeu de Nim pour se détendre Allez terminons cet article par une note légère. Parlons du jeu de Nim aussi appelé, le jeu des bâtonnets. Ce jeu a été notamment popularisé en France par l'émission Fort Boyard. Il s'agit d'un jeu se jouant avec un ensemble de petits bâtonnets. Tour à tour les deux joueurs doivent en retirer 1, 2 ou 3 et celui qui retire le dernier perd la partie. Là vous vous demandez certainement ce que vient faire cette Appendice dans cet article. Eh bien disons qu'il s'agit d'une tradition... Je ne connais en effet aucun livre sérieux parlant de résolution de jeu qui ne parle pas à un moment ou un autre du jeu de Nim, car ce jeu et ses variantes sont en effet à la base de la théorie combinatoire des jeux. Le jeu de Nim est résolu et contrairement aux jeux précédent cités dans cet article, cette résolution a été obtenue sans avoir recours à la puissance du calcul informatique. Dans ce cas précis, la stratégie pour gagner consiste à laisser toujours à votre adversaire un nombre de bâtonnets de la forme 4n+1 lorsque c'est à lui de jouer. Ce qui est au final étonnant avec le jeu de Nim, c'est qu'il peut être perçu comme une sous-partie de Magic ! Il est en effet théoriquement possible de mettre deux joueurs dans une situation de jeu à Magic où ils sont forcés de jouer à un jeu de Nim. Pour cela il suffit que chaque joueur contrôle Ensnaring Bridge, 2 Carnophage,Fretwork Colony, Axis of Mortality, Recycle et qu'aucun joueur n'ait de cartes en main. Les joueurs ne piochent pas, ne peuvent pas attaquer et ne peuvent rien jouer. Les seuls actions qu'ils vont pouvoir faire vont se passer à leur entretien et vont concerner les Carnophage et Axis of Mortality qu'ils contrôlent. Ici c'est le total de points de vie des deux joueurs qui va nous intéresser. Tour à tour, les joueurs vont pouvoir à l'entretien diminuer ce total de point de vie de 1, 2 ou 3 grâce à Carnophage, Fretwork Colony et Axis of Mortality. Lorsqu'il ne restera plus qu'un point de vie à chaque joueur, le prochain joueur dont c'est l'entretien ne pourra plus perdre de point de vie sans perdre la partie. On a donc bien construit un jeu de Nim dans une partie de Magic où le nombre de points de vie total correspond au nombre de bâtonnets augmenté de un. On peut aussi créer tout un tas de variantes du jeu de Nim : - en multipliant bien entendu les Carnophage et Fretwork Colony - en rendant le jeu asymétrique - en ajoutant des joueurs et des Axis of Mortality - en utilisant d'autres cartes marrantes comme : Oath of Mages, Subversion, Vampire Lacerator, ou encore Triskaidekaphobia. Après j'ai un faible personnellement pour les versions qui utilisent : Bitterblossom + Vile Consumption puisqu'ici le nombre d'options qui s'offrent aux joueurs peut changer à chaque tour. Liens externes : - Magic : the Gathering is Turing Complete : La publication scientifique originale qui a inspiré cet article. - Accidentally Turing-Complete : Quelques jeux et systèmes qui se sont avéré contre toute attente Turing-complet (à l'intérieur desquels ont peut construire une Machine de Turing). - Chaine Youtube DeepMind : Les cinq parties de Lee Sedol contre AlphaGo filmées. - Comment DeepMind a entrainé son I.A. pour battre des champions ... - Checkers is Solved : La publication scientifique affirmant que le jeu de dame 8x8 a été résolu. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






